By Jian-Qiao Zhu

Human behavior is famously variable across all kinds of judgments and decisions, so pinning down “laws” of human behavior is much tougher than writing the laws of physics, such as gravity or thermodynamics.¹ Today, though, psychologists and economists have a powerful new toolkit for better discovering the principles behind human behavior: large-scale online experiments paired with machine-learning models. In our new Nature Human Behaviour paper, we put that toolkit to work on strategic decisions in economic games.

A Typical Matrix Game

To illustrate the kind of experimental task we’re studying, consider a simple payoff matrix like the one shown in Figure 1. In this task, our participants act as the row player, choosing between two options, A or B. Their potential payoffs are shown in blue. Each row player is paired, randomly and anonymously, with another participant (the column player) from the same online platform. This column player then chooses between two options, C or D, with their payoffs marked in red.

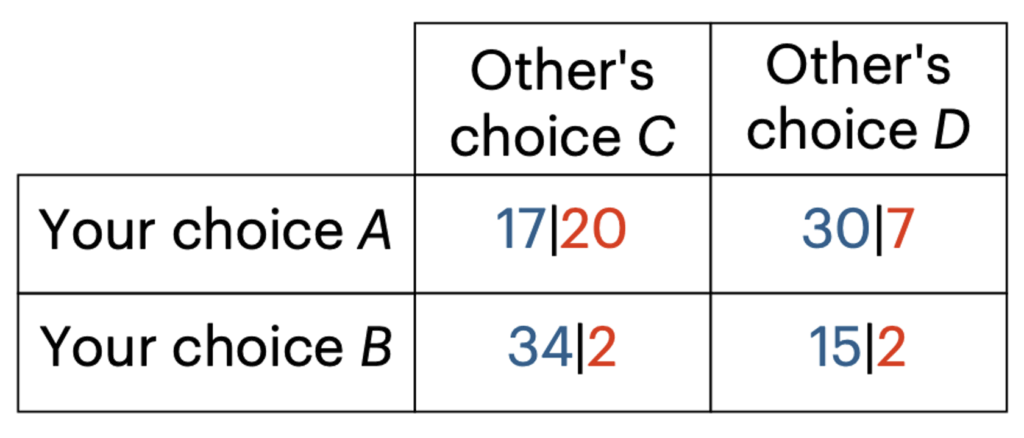
Here’s how a single game plays out: If you (as the row player) pick A and your opponent (column player) picks C, the outcome is the top-left cell of the 2-by-2 matrix. That is, you earn 17 points, and your opponent earns 20 points. At the end of the study, participants earn real money based on one randomly selected game, with every 100 points translating to $1 in bonus pay.

Our Three-Step Pipeline

Now, here’s our recipe to leverage modern tools to uncover hidden laws behind strategic behavior:

1. Scale up data collection. Crowdsourcing platforms let researchers gather thousands—even millions—of decisions from online participants playing carefully designed games.
2. Let a neural network automatically discover the right function. Feed the game features and participants’ choices into a neural network. Its job is to discover the best possible mapping from “what the player sees” (i.e., experimental stimuli) to “what the player does” (i.e., human behavior), capturing as much behavioral variation as it can.
3. Open the black box. At first glance, the network’s learned rules may look opaque. But modern interpretability tools allow researchers to peek inside and ask: Which aspects of the game make it feel harder or easier? Which cues do players rely on most?

Importantly, once the neural network reliably mimics how people play, we don’t have to run a fresh experiment for every new “what-if” game scenario. Instead, we can directly explore the neural network, treating it like a stand-in for the average person’s mind. By examining how this model processes matrix games, we aim to uncover cognitive theories about why some games feel intuitive, while others make our heads spin.

Using Neural Networks to Develop Theories of Strategic Choices

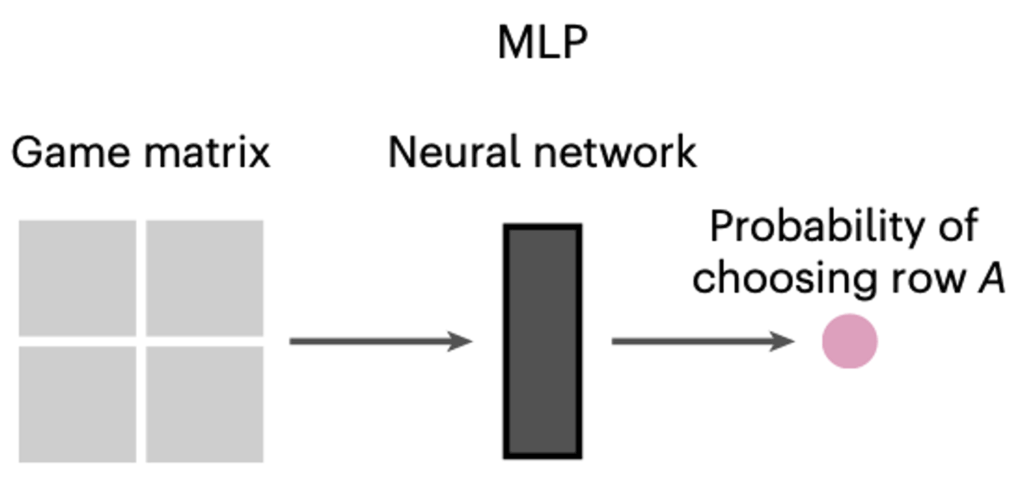
In our study, we generated more than 2,400 different 2-by-2 matrix games and collected over 90,000 human decisions about these games. Using this data, we built a neural network model (see Figure 2) that accurately predicts how people will play these games, explaining about 92 percent of the variance in people’s choices when tested on choices in held-out games.

Next, we gradually introduced more structure, inspired by existing models from behavioral game theory (e.g., level-k thinking and quantal response function), to the neural-network model. These behavioral theories suggest that people don’t always make perfectly rational choices. Instead, they might reason only a few steps ahead (this limited thinking depth is called level-k thinking) or respond with some degree of randomness (this noise in their ability to best respond is the quantal response function).

By embedding these structures directly into the neural network, we constrained its predictions, reducing flexibility but gaining clearer theoretical insights. In these models, the final prediction is generated by a behavioral model (e.g., a level-2 quantal response model; see Figure 3), but with a twist: The model’s parameters are not fixed. Instead, they are produced by a neural network that takes the game matrix as input. This allows the model to adapt its predictions to the specific features of each game, while still staying grounded in the assumptions of behavioral game theory.

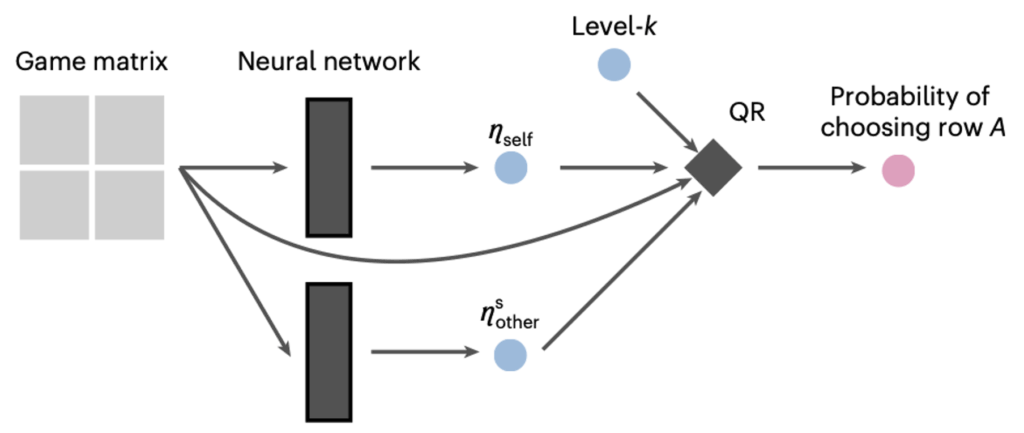
One of our best-performing structured neural-network models assumed that people typically reason two steps ahead (level-2), but with two key types of noise: (i) noise in their own calculations of the best move, and (ii) noise in belief about the opponent’s ability to best respond. Despite these structural constraints, this model explained about 88 percent of the variance in human decisions, close to the 92 percent explained by the fully flexible, unconstrained neural network.

Searching for Game Complexity

The reason our structured neural network model performs so well is that it allows the two noise terms—behavioral noise and belief noise—to adjust based on each individual game. These context-dependent effects, where the level of noise varies from game to game, are precisely what traditional behavioral models fail to capture. It’s hard to describe precisely why these noises change from one game to another using simple rules alone. Instead, we rely on neural networks trained on huge datasets of human decisions to capture these subtle variations. Still, it would be incredibly valuable to understand why certain games are considered noisier by the structured neural network model, since this variation is exactly what allows the model to more accurately predict people’s strategic choices.

A promising idea is to connect the noisiness in human behavior directly to the complexity of the games themselves. Intuitively, people find it harder to play rationally when games are complex, leading to noisier decisions. To pinpoint what drives the noise predicted by our neural-network models, we ran a LASSO regression to see how different game features influence noisiness (Figure 4a).

We discovered three key features of the game matrix that stand out as predictors of noisiness:

1. Payoff Dominance: Whether the payoff at the Nash equilibrium clearly beats every other possible outcome. If there’s such an outcome, the game is simpler.
2. Arithmetic Difficulty: How challenging it is to compute the expected payoff differences between the player’s two strategies. Games requiring difficult mental calculations are more complex.
3. Thinking Depth: The minimum number of reasoning steps players must take to reach a rational decision. The more steps required, the more complex the game is.

In other words, these three features of a game matrix significantly affect how complex people find a game, influencing the noisiness of their responses.

Using these findings, we developed a practical “Game Complexity Index.” This index takes any matrix game as input and outputs a complexity rating, predicting how complex players will find it. When the complexity rating is high, players’ choices tend to become more random, hovering near a 50/50 chance rather than clearly favoring one option over another (Figure 4b).

Additionally, we found that higher complexity ratings correlated with longer response times (Figure 4d), meaning players took more time to think when faced with more complicated games.

This complexity index also proved useful beyond our initial dataset (Figure 4c and 4e). It successfully predicted human behavior in a follow-up study with new participants and different games, demonstrating its generalizability.

Summary

In short, machine learning and AI don’t replace traditional experiments and theory-building in economics and psychology—they supercharge them. By harnessing powerful computational tools, we turn mountains of messy human data into clear, actionable insights about how we think, decide, and play.

1. My co-author and postdoc advisor, Tom Griffiths, explores this topic in depth in his forthcoming book, The Laws of Thought: The Quest for a Mathematical Theory of the Mind. ↩︎